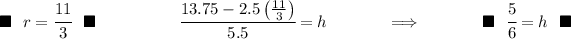Question

A cylinder is inscribed in a right circular cone of height 2.5 and radius (at the base) equal to 5.5. what are the dimensions of such a cylinder which has maximum volume?

Answer 1

Check the picture below.

so hmm if we look at the cone straight from the front and check a cross-section of it, it'd look like the cross-section of the right-hand-side of the picture.

Now, with the cylinder having radius "r" and height "h", those two triangles we see in greenish color are similar, thus we can use proportions to correlate "h" and "r", so let's do that.

`\cfrac{2.5-h}{r}~~ = ~~\cfrac{h}{5.5-r}\implies 13.75-5.5h-2.5r+rh=rh \\\\\\ 13.75-2.5r=5.5h\implies \boxed{\cfrac{13.75-2.5r}{5.5}=h}`

now, let's plug that in the volume of the cylinder's equation

`V(r)=\pi r^2\cdot \cfrac{13.75-2.5r}{5.5}\implies V(r)=\cfrac{\pi }{5.5}(13.75r^2-2.5r^3) \\\\\\ \cfrac{dV}{dr}=\cfrac{\pi r(27.5-7.5r)}{5.5}\hspace{5em}0~~ < ~~r ~~ < ~~ 2.5`

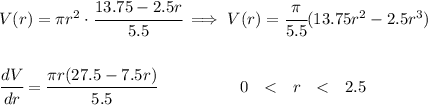
now, our "r" variable can't be 0 or 2.5, as the cylinder tiptoes up and down, because if that ever happens, our cylinder's volume goes poof.

`0=\cfrac{\pi r(27.5-7.5r)}{5.5}\implies 0=27.5-7.5r\implies 7.5r=27.5 \\\\\\ r=\cfrac{27.5}{7.5}\implies r=\cfrac{11}{3}`

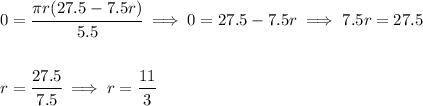
the way I do region testing for the 1st derivative, is I usually grab the critical point and subtract hmm say 0.0000001 from it and put it in a variable in my calculator, then I add 0.0000001 to it and put it in another variable, then I use that variable in the 1st derivative calculation. Anyhow, doing so and running a 1st derivative test, we'd see that the region to the left of 11/3 is positive whilst the region to the right is negative, as you can see in the picture at the bottom, yielding a maximum extremum, r = 0 is another critical point but as we noticed the constraints is out of bounds, so not in consideration.

so V(r) is at a maximum when r = 11/3

`\blacksquare~~ r=\cfrac{11}{3} ~~\blacksquare \hspace{5em} \cfrac{13.75-2.5\left( (11)/(3) \right)}{5.5}=h~\hfill \implies ~\hfill \blacksquare~~ \cfrac{5}{6}=h ~~\blacksquare`