Answer:
(a) The price of the pen is $1.4
(b) The price of the ruler before the increase is $1.05
Explanation:
∵ The ratio of the price of a pen to the price of a ruler is 4: 3
→ Multiply each term of the ratio by m, where m is a constant
∴ The cost of the pen = 4m
∴ The cost of the ruler = 3m
∵ The price of a ruler increases by 70p
→ Change 70 p to dollars by divide it by 100
∴ The price of a ruler increases by $0.7
∵ The old price of the ruler = 3m
∴ The new price of the ruler = 3m + 0.7
∵ The ratio between the pen and the ruler becomes 4: 5
∴ The price of the pen/the new price of the ruler =
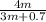
∴ The new ratio of the prices =
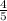
→ Equate the fraction of the ratio by the fraction of the prices
∴
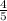 =
=
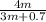
→ By using cross multiplication
∵ 5 × (4m) = 4 × (3m + 0.7)
∴ 20m = 4(3m) + 4(0.7)
∴ 20m = 12m + 2.8
→ Subtract 12 m from both sides
∴ 8m = 2.8
→ Divide both sides by 8 to find m
∴ m = 0.35
(a)
∵ The price of the pen = 4m
∵ m = 0.35
∴ The price of the pen = 4(0.35)
∴ The price of the pen = $1.4
(b)
∵ The price of the ruler before the increase = 3m
∵ m = 0.35
∴ The price of the ruler before the increase = 3(0.35)
∴ The price of the ruler before the increase = $1.05