Answer:
There are 7 terms in the GP
Explanation:
In the geometric progression, there is a constant ratio between each two consecutive terms
The rule of the nth term of the geometric progression is
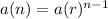 , where
, where
- n is the position of the term in the sequence
∵ The first term = 5

∴ a = 5

∵ The last term =
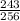
∴ a(n) =
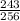
∵ The common ratio =

→ Substitute these values in the rule above to find n
∵
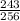 = 5
= 5
 .
.
![[(3)/(4)]^(n-1)](https://img.qammunity.org/2021/formulas/mathematics/high-school/ek4u3r0p59zweigphdrxxur8108fh5laiv.png)
→ Divide both sides by 5

∴
 =
=
![[(3)/(4)]^(n-1)](https://img.qammunity.org/2021/formulas/mathematics/high-school/ek4u3r0p59zweigphdrxxur8108fh5laiv.png)
→ Let us find how many 3 in 729
∵ 729 ÷ 3 = 243 ÷ 3 = 81 ÷ 3 = 27 ÷ 3 = 9 ÷ 3 = 3 ÷ 3 = 1
∴ There are 6 three in 729
∴ 729 =
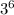
→ Let us find how many 4 in 4096
∵ 4096 ÷ 4 = 1024 ÷ 4 = 256 ÷ 4 = 64 ÷ 4 = 16 ÷ 4 = 4 ÷ 4 = 1
∴ There are 6 four in 4096
∴ 4096 =

∵
 =
=
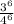 =
=
![[(3)/(4)]^(6)](https://img.qammunity.org/2021/formulas/mathematics/high-school/ai719v8wk7xxcmovs7g4hcg4swg9822pya.png)
∴
![[(3)/(4)]^(6)](https://img.qammunity.org/2021/formulas/mathematics/high-school/ai719v8wk7xxcmovs7g4hcg4swg9822pya.png) =
=
![[(3)/(4)]^(n-1)](https://img.qammunity.org/2021/formulas/mathematics/high-school/ek4u3r0p59zweigphdrxxur8108fh5laiv.png)
∵ The bases are equal
∴ Their exponents are equal
∴ 6 = n - 1
→ Add 1 to both sides
∴ 6 + 1 = n - 1 + 1
∴ 7 = n
∴ There are 7 terms in the GP