Question

The perimeter of a triangular garden is 900cm and its sides are in the ratio 3 : 5 : 4. Using Heron’s formula, find the area of the triangular garden?

Answer 1

The area of the triangular garden is 33750 cm²

Explanation:

Let us use Heron's Formula for the area of a triangle

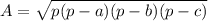`A=√(p(p-a)(p-b)(p-c))`, where

• a, b, and c are the lengths of the three sides of the triangle

• 
  `p=(a+b+c)/(2)`

∵ The perimeter of a triangular garden is 900 cm

∴ The sum of the lengths of its three sides = 900 cm

∵ Its sides are in the ratio 3 : 5 : 4

→ Let us use the ratio method to find the length of its sides

→ S1 : S2 : S3 : perimeter

→ 3 : 5 : 4 : 12 ⇒ (3 + 5 + 4)

→ a : b : c : 900

→ By using cross multiplication

∵ a × 12 = 3 × 900

∴ 12a = 2700

→ Divide both sides by 12

∴ a = 225 cm

∵ b × 12 = 5 × 900

∴ 12b = 4500

→ Divide both sides by 12

∴ b = 375 cm

∵ c × 12 = 4 × 900

∴ 12c = 3600

→ Divide both sides by 12

∴ c = 300 cm

Now let us use Heron’s formula, to find the area of the triangular garden

∵
`p=(a+b+c)/(2)`

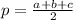
∵ a = 225, b = 375, c = 300

∴
`p=(225+375+300)/(2)=(900)/(2)`

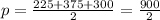
∴ p = 450

∵
`A=√(450(450-225)(450-375)(450-300))`

∴ A = 33750 cm²

∴ The area of the triangular garden is 33750 cm²