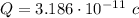Question

A parallel-plate capacitor has an area of 4.0 cm^2, and the plates are separated by 1.0 mm.

a. What is the capacitance?
b. How much charge does this capacitor store when connected to a 9.0 V battery?

Answer 1

`C=3.54\cdot 10^(-12)\ F`

`Q=3.186\cdot 10^(-11)\ c`

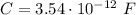
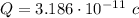
Step-by-step explanation:

Capacitance of a parallel-plate capacitor

The parallel plate capacitor consists of two identical conducting plates, each having a surface area A, separated by a distance d with no material between the plates.

The capacitance of the capacitor can be calculated as follows:

`\displaystyle C=\epsilon_o(A)/(d)`

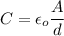
Where
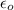`\epsilon_o` is the permittivity of free space. Its numerical value in SI units is:

`\epsilon_o=8.85 \cdot 10^(-12)\ F/m`

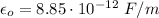
a.

The capacitor of the question has an area of A=4 cm^2 and the plates are separated by d=1 mm. Both magnitudes must be converted to SI:

`\displaystyle A=4\ cm^2\left((1\ m)/(100\ cm)\right)^2=4\cdot 10^(-4)\ m^2`

`\displaystyle d=1\ mm(1\ m)/(1000\ mm)=1\cdot 10^(-3)\ m`

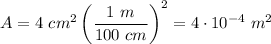
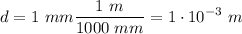
Now calculate the capacitance:

`\displaystyle C=8.85 \cdot 10^(-12)(4\cdot 10^(-4)\ m^2)/(1\cdot 10^(-3)\ m)`

`C=3.54\cdot 10^(-12)\ F`

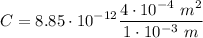
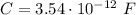
b.

The charge Q stored in any capacitor C when a voltage V is applied is given by the equation:

Q = CV

Entering the known values into this equation gives:

`Q = 3.54\cdot 10^(-12)\cdot 9`

`Q=3.186\cdot 10^(-11)\ c`