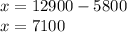Question

Daisy invests a total of $12900 in two accounts. One account pays 9% annual interest and the other pays 8% annual interest. If the total annual interest from both accounts is $1103, how much was invested in each account? Suppose x is the amount invested at 9% and y is the amount invested at 8%. Find an answer question above using a system of linear equations of x and y. List the equations in that system.

Answer 1

The equations:

`x + y = 12900\\.09x + .08y = 1103`

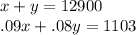
the value for x and y:

`x = 7100\\y = 5800`

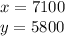
Explanation:

invest amount = 12900

let x = amount put into the first account

let y = amount put into the second account

we know the sum of of both is 12900, thus

`x + y = 12900`

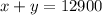
We also know the sum of their annual interest rate is 1103

`.09x + .08y = 1103`

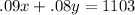
Thus the equations needed are

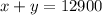`x + y = 12900` and
`.09x + .08y = 1103`

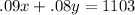
To find the values for x and you know have all equations you need

we need to get this equation
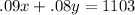`.09x + .08y = 1103` to a single variable

we can do this using x or y, lets use x

we know

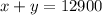`x + y = 12900`, so

`x = 12900 - y`

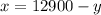
lets plug
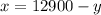`x = 12900 - y` into
`.09x + .08y = 1103`

`.09(12900 - y) + .08y = 1103`

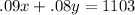
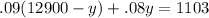
1161 - .09y + .08y = 1103

-.01y = -58

y = 5800

we can get x from this equation
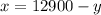`x = 12900 - y` from above

`x = 12900 - 5800\\x = 7100`