Question

A King in ancient times agreed to reward the inventor of chess with one grain of wheat on the first of the 64 squares of a chess board. On the second square the King would place two grains of​ wheat, on the third​ square, four grains of​ wheat, and on the fourth square eight grains of wheat. If the amount of wheat is doubled in this way on each of the remaining​ squares, how many grains of wheat should be placed on square 24 ​? Also find the total number of grains of wheat on the board at this time and their total weight in pounds.​ (Assume that each grain of wheat weighs​ 1/7000 pound.)

Answer 1

1) 8,388,608 grains of wheat.

2) 16,777,215 grains of wheat.

3) 239,674.5 pounds.

Explanation:

Question 1)

We know that on the first square, there is 1 grain of wheat.

On the second, 2 grains of wheat.

On the third, 4 grains of wheat.

And on the fourth, 8 grains of wheat.

Therefore, we have a geometrically increasing sequence. It looks like:

1, 2, 4, 8...

Therefore, to find the number of grains on the 24th square, we can write an explicit formula.

The standard form for the explicit formula for a geometric sequence is:

`x_n=a(r)^(n-1)`

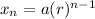
Where a is the initial amount, r is the common ratio, and n is the nth term (starting from 1).

We know that the initial term a is 1 because there’s one grain of wheat on the first square.

And the common ratio will be 2 because each square has double the amount of the previous square.

So, substitute 1 for a and 2 for r. This yields:

`x_n=1(2)^(n-1)\\`

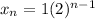
We can simplify this:

`x_n=2^(n-1)`

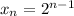
So, to find the amount of wheat on the 24th square, we simply need to substitute 24 for n and evaluate. So:

`x_(24)=2^(24-1)=2^(23)`

Evaluate. Use a calculator:

`x_(24)=8,388,608`

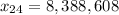
Therefore, on the 24th square, there are 8,388,608 grains of wheat.

Question 2.1)

We want to find the total number of grains of wheat on the board at this time.

In other words, we want to find the sum of our geometric sequence when n is 24.

The formula for the sum of a geometric series is:

`S_n=(a(r^n-1))/(r-1)`

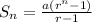
Where rⁿ is the value of the number of terms n, r is the common ratio, and a is the initial term.

We want to find the sum after 24 times. So, n is 24.

So, substitute 24 for n, 2 for r, and 1 for a. This yields:

`S_(24)=((1)(2^(24)-1))/(2-1)`

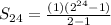
Evaluate. Use a calculator:

`S_(24)=16, 777, 215`

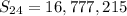
Therefore, the total sum of the number of grains of wheat at the board at the 24th square is 16,777,215.

Question 2.2)

And to find the weight, we will just have to multiply our total amount by 1/7000. So:

`W=16777215((1)/(70))`

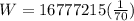
Use a calculator:

`W=239,674.5\text{ lbs}`

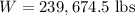
So, the total weight is 239,674.5 pounds.