Answer:
x = 21°, y = 42°, TQ = 3.75 cm
Explanation:
In Δ SRT
∵ m∠RST = 21°, m∠STR = 117°
∵ The sum of the measures of the interior angles of a triangle is 180°
∴ m∠RST + m∠STR + m∠SRT = 180°
∴ 21° + 117° + m∠SRT = 180°
→ Add the like angles
∴ 138° + m∠SRT = 180°
→ Subtract 138° from both sides
∴ m∠SRT = 42°
In the given circle
∵ ∠SRP and ∠SQP are inscribed angles subtended by the arc SP
→ Inscribed angles subtended by the same arc are equal in measures
∴ m∠SRP = m∠SQP ⇒ (1)
∵ m∠SRP = 42° , m∠SQP = y
∴ y = 42°
∵ ∠RSQ and ∠RPQ are inscribed angles subtended by the arc RQ
→ Inscribed angles subtended by the same arc are equal in measures
∴ m∠RSQ = m∠RPQ ⇒ (2)
∵ m∠RSQ = 21° , m∠RPQ = x
∴ x = 21°
∵ The chord SQ intersects the chord PR at the point T
∴ ∠STR and ∠PTR are vertically opposite angles
→ The vertically opposite angles are equal in measures
∴ m∠STR = m∠PTR ⇒ (3)
→ From (1), (2), and (3) the two triangles SRT and PQT are similar using
AAA postulate of similarity
∴ Δ SRT ≈ ΔPQT ⇒ AAA postulate
∴ Their sides are proportion
∴
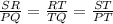
∵ SR = 8.32 cm, PQ = 9.43 cm, RT = 3.31 cm
→ Substitute them in the ratio above
∴
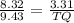
→ By using cross multiplication
∴ TQ × 8.32 = 9.43 × 3.31
→ Divide both sides by 8.32 to find TQ
∴ TQ =
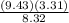
∴ TQ = 3.751598558
→ Round it to 2 d.p
∴ TQ = 3.75 cm