Answer:
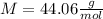
Step-by-step explanation:
Hello.
In this case, knowing the temperature, density and temperature of Y which behaves ideally, we can write the ideal gas equation:
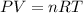
Whereas the moles are equal to the mass over the molar mass of Y:
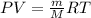
Thus, solving for the molar mass we write:

Yet, since density is mass of over volume, we then write:
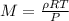
Considering the pressure in atm and the density in g/L:
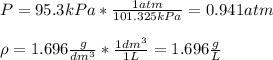
Therefore, by plugging the values in, we obtain:
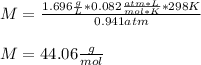
Thus, the gas may be propane (
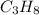 ) since it molar mass is 44.11 g/mol.
) since it molar mass is 44.11 g/mol.
Best regards!