Answer:
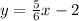
Explanation:
Point-slope form:
where
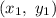 are coordinates of a point that the line passes through, and
are coordinates of a point that the line passes through, and
 is the slope of the line.
is the slope of the line.
We are given two points that the line passes through, but we are not given the slope.
We can find the slope by using the slope formula:
where
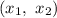 and
and
 are two points that the line passes through.
are two points that the line passes through.
Substitute (-6, -7) and (6, 3) into the slope formula:
The slope of this line is 5/6. Now we are able to use the point-slope equation to find the slope-intercept equation
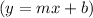 of this line.
of this line.
Substitute a point that the line passes through and the slope of the line into the point-slope equation. I'm using the point (6, 3).
Distribute 5/6 inside the parentheses.
Add 3 to both sides of the equation.
This is the equation of the line that passes through (-6, -7) and (6, 3) in slope-intercept form.