Question

12. An object is fired from the top of a 200 ft. tower with an initial velocity of 80 ft/sec. and is

modeled by the equation h(t) = -16t^2+80t + 200.

a) How long after firing does it reach its maximum height?

b) What is the maximum height?

Answer 1

a) The object reaches its maximum height at t=2.5 seconds

b) The maximum height is 300 m

Explanation:

Maximum Value of a Function

First derivative criteria:

If f(t) is a real continuous function of t and the first derivative of f called f'(t) exists, then solving the equation:

f'(t)=0

Gives the critical points of f, some of which could be maximum or minimum.

Second derivative criteria:

If t=t1 is a critical point of f(t) and the second derivative of f:

f''(t1) is positive, then t1 is a minimum of f

f''(t1) is negative, then t1 is a maximum of f.

f''(t1)=0, no conclusion can be drawn.

The height of the object is modeled by the function:

`h(t) = -16t^2+80t + 200`

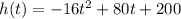
a)

To find the maximum height, we use the above criteria.

Find the first derivative:

h'(t) = -32t+80

Equate h'(t)=0

-32t+80=0

Solve:

`-32t=-80`

`t=80/32=2.5`

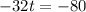
t=2.5 seconds

Find the second derivative:

h''(t)=-32

Since the second derivative is negative, the critical point is a maximum.

The object reaches its maximum height at t=2.5 seconds

b) Evaluate h(2.5)

`h(2.5) = -16\cdot 2.5^2+80\cdot 2.5 + 200`

`h(2.5) = -100+200 + 200`

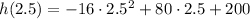
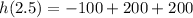
h(2.5)=300 m

The maximum height is 300 m