Question

Your 6 1/4 - year investment of 40,000 at 14% compounded quarterly is worth how much now?​

Answer 1

The investment of $40,000 is worth $94,529.80 now

Explanation:

Compound Interest

It occurs when the interest is reinvested along with the principal, rather than paying it out. When it happens interest in the next period is then earned on the principal sum plus previously accumulated interest.

To calculate the final amount we use:

`{\displaystyle A=P\left(1+{\frac {r}{n}}\right)^(nt)}`

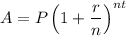
Where:

A = final amount

P = initial principal balance

r = interest rate

n = number of times interest applied per time period

t = number of time periods elapsed

The investment is for t=6 1/4 years = 6.25 years with an initial balance of P=40,000 at a rate r=14% = 0.14 compounded quarterly. Since there are 4 quarters per year, then n=4.

Applying the formula:

`{\displaystyle A=40,000\left(1+{\frac {0.14}{4}}\right)^(4*6.25)}`

`{\displaystyle A=40,000\left(1+0.035\right)^(25)}`

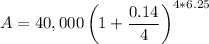
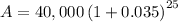
A=$94,529.80

The investment of $40,000 is worth $94,529.80 now