Question

Given a 30-60-90 triangle with a hypotenuse of 11 mm solve for the other sides. (Explain)

Answer 1

Need a calculator

Explanation:

This will be hard to explain without the ability to draw an example.

The one thing you can memorize is SOH - CAH - TOA

This stands for SIN(Opposite/Hypotenuse), COS(Adjacent/Hypotenuse) and TAN(Opposite/Adjacent).

When you know the angles of a right triangle and at least one side length, you can get the length of all the sides.

So a right triangle has two legs (sides) and the hypotenuse. If you use the first angle ( 30 degrees) you can use the formulas above to calculate the side length.

Pick either the SOH or the CAH. Let's use SOH and write out the equation:

SIN(30 degrees) = Opposite Side divided by the Hypotenuse (11mm)

You can solve for the Opposite Side by multiplying both sides of the equal sign with 11mm. You end up with SIN(30 degrees) X 11m = Opposite Side.

So the side directly across from the 30 degree angle should be 5.5mm

You can do the exact same thing with the 60 degree angle.

SIN(60 degrees) = Opposite Side divided by Hypotenuse (11mm) OR

SIN(60 degrees) X 11mm = Opposite Side

This comes out to about 9.5mm

You can check the math by using the other equation CAH

Start with the 30 degree angle and solve for the adjacent side. This is the side that is touching the 30 degree angle. Equation will be

COS(30 degrees) X 11mm = Adjacent Side or about 9.5mm

The other equation will give you the side that is touching the 60 degree angle.

COS(60 degrees) X 11mm = Adjacent Side or 5.5mm

You can also use one last thing to check your math. The Pathagorean Theorem says in a right triangle
`A^(2)` +
`B^(2)` =
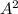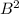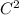`C^(2)` where C is the hypotenuse and A and B are the two sides.

`5.5^(2)` +
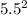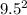`9.5^(2)` should equal
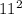`11^(2)`. Give or take a few decimal places, it's almost exactly 11 (10.977 to be exact).