Question

Given m || n, find the value of x and y.
(3x-4)
(6x-5)

Answer 1

X=21 and Y=121

Explanation:

With these types of problems, we need to know our vertical angles and that lines are 180° when two angles on a line are next to each other.

To solve this problem algebraically we want to add (3x-4) and (6x-5) together so that they equal 180. The reason we do this is that they lie on the same line which is 180°. The equation would look like
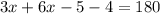`3x+6x-5-4=180`. We then want to add like terms which will leave us with
`9x-9=180`. Now we want to get 9x by itself by adding 9 on each side which leaves us with
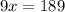`9x=189`. To isolate x we need to divide on each side by 9 which finally leaves us with
`x=21`

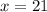
Now that we have the value of x (21) we can now utilize our knowledge of vertical angles (angles that are completely across and equal to one another.) We can find y by doing this equation:
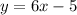`y=6x-5` and with the value of x found we can plug in the value to get
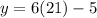`y=6(21)-5` which simplifies to
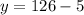`y=126-5` then to
`y=121`.