Answer:
About 6 cents per minute
Explanation:
Looking at the actual minutes and cost of the plan you can see this. Let's start with the first minutes given (100 with $14) which then goes to 200 with $20. There is a difference of 100 between the two and a difference of 6 with 14 and 20. If you would do 100*0.06 (6 cents) then you would see that for every 100 minutes there would be $6 being paid, in which is the difference between all the bottom numbers when going from left to right.
A more algebraic way to do this is by finding the slope from points we can make from the table (for example 100,14 , 200,20 , 300,26...). now let;s find the slope in which the two points (100,14) and (200,20) share. Using the slope formula
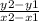 we substitute in our values so that the new equation would look like
we substitute in our values so that the new equation would look like
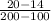 which when adding like terms makes it
which when adding like terms makes it
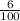 or in this case 0.06. The slope would be 0.06 and therefore every minute that is on the phone, $0.06 will be added to the bill.
or in this case 0.06. The slope would be 0.06 and therefore every minute that is on the phone, $0.06 will be added to the bill.