Question

PLZ ANSWER QUICK:

The graph shows two lines, A and B:

A graph is shown with x- and y-axes labeled from 0 to 6 at increments of 1. A straight line labeled A joins the ordered pair 3, 0, and the ordered pair 0, 6. Another straight line labeled B joins the ordered pair 0, 0, and the ordered pair 5, 5.

Based on the graph, which statement is correct about the solution to the system of equations for lines A and B?
0, 6) is the solution to both lines A and B.
(0, 6) is the solution to line B but not to line A.
(2, 2) is the solution to both lines A and B.
(2, 2) is the solution to line A but not to line B.

Answer 1

Answer: Choice D

(2,2) is the solution to line A, but not to line B

==========================================================

Step-by-step explanation:

Let's find the equation of line A

First we need the slope

m = (y2-y1)/(x2-x1)

m = (6-0)/(0-3)

m = 6/(-3)

m = -2

Since the point (0,6) is on line A, we know b = 6 is the y intercept.

The equation of line A is y = -2x+6.

-----------------------------

Let's find the equation for line B

So we need the slope

m = (y2-y1)/(x2-x1)

m = (5-0)/(5-0)

m = 5/5

m = 1

The y intercept is b = 0 since the line goes through (0,0)

The equation of line B is y = 5x+0 which is the same as y = 5x.

------------------------------

Our system of equations is

`\begin{cases}y = -2x+6\\y = 5x\end{cases}`

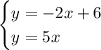
We can see that plugging x = 0 into line A's equation leads to y = 6. So (0,6) is on line A. However, the point (0,6) is not on line B because plugging x = 0 leads to y = 0.

This allows us to rule out choices A and B.

--------------------------------

Let's see what happens when we plug in x = 2 to line A

y = -2x+6

y = -2*2+6

y = -4+6

y = 2

The point (2,2) is on line A

Now let's do the same for line B

y = 5x

y = 5*2

y = 10

The point (2,10) is on line B meaning that (2,2) is not on line B.

We can rule out choice C and conclude that choice D is the final answer.

Side note: Choice D should read "(2,2) is a solution" instead of "(2,2) is the solution" since there are infinitely many solutions on any given line. So another solution for example would be (0,6).