Answer: Choice A
-20, -10, 0, 10, and 20 only
In other words, everything but -30.
========================================================
Step-by-step explanation:
Let's solve for x
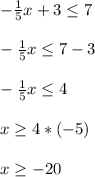
Note how the inequality sign flips when we multiply both sides by the negative number.
Since x can be -20 or larger, this means that the values -20,-10,0,10,20 are all solutions. Only -30 is a non-solution. It might help to draw out a number line to see which values work and don't work.
--------------------------------
An alternative method is to plug each value from the set {-30,-20,-10,0,10,20} into the original inequality and simplifying. If you get a true statement at the end, then the value is a solution.
I'll show an example with x = -30 and x = -20 to show a non-solution and a solution. I'll let you check the others.
So let's start with x = -30

The last statement is false because 9 is not 7 or smaller than 7. So that's why x = -30 is not a solution.
Now let's try x = -20
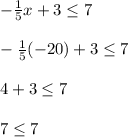
This is a true statement since any number is equal to itself.
You should find that x = -10, x = 0, x = 10, and x = 20 lead to true statements.