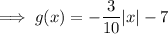Question

NO LINKS!!!! Please help me with this graph. Part 7a​

Answer 1

`g(x)=-(3)/(10)|x|-7`

Step-by-step explanation:

Translations

For
`a > 0`

`f(x)-a \implies f(x) \: \textsf{translated}\:a\:\textsf{units down}`

`y=a\:f(x) \implies f(x) \: \textsf{stretched parallel to the y-axis by a factor of}\:a`

`y=-f(x) \implies f(x) \: \textsf{reflected in the} \: x \textsf{-axis}`

-----------------------------------------------------------------------------------------

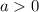
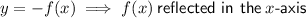
Parent function:
`f(x)=|x|`

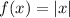
From inspection of the graph, the transformed function has been reflected in the x-axis.

`\implies -f(x)=-|x|`

The vertex of the parent function is the origin (0, 0). The vertex of the transformed function is at (0, -7). Therefore, there has been a translation of 7 units down.

`\implies -f(x)-7=-|x|-7`

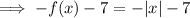
From inspection of the graph, we can see that it has been stretched parallel to the y-axis:

`\implies -a\:f(x)-7=-a|x|-7`

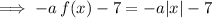
The line goes through point (10, -10)

Substituting this point into the above equation to find
`a`:

`\implies -a|10|-7=-10`

`\implies -10a=-3`

`\implies a=(3)/(10)`

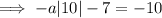
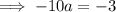
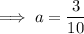
Therefore,

`\implies g(x)=-(3)/(10)|x|-7`

Answer 2

`\large \boxedx-0\right`

Step-by-step explanation:

Absolute value of a graph formula:

• y = a |x -h| + k

Identify the vertex : (h, k) = (0, -7)

As the graph opens downward, take negative/fall coordinates.

Two points: (0, -7), (10, -10)

`\sf Find \ slope \ (a) : \sf \ (y_2 - y_1)/(x_2- x_1) \ = \ (-10-(-7))/(10-0) \ = -0.3`

Put them together:
`\bf y = -0.3|x - 0| -7 \ \ \ \approx \ \ y = -0.3|x| - 7`