1 Answer

Tehaaron · Answer 1 · 2021-01-31T15:42:43+0000

Given:

The base area of a right circular cone is
(1)/(4) of its total surface area.

To find:

The ratio of the radius to the slant height.

Solution:

We know that,

Area of base of a right circular cone =
$\pi r^2$

Total surface area of a right circular cone =
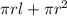
$\pi rl+\pi r^2$

where, r is radius and l is slant height.

According to the question,

$\pi r^2=(1)/(4)(\pi rl+\pi r^2)$

Multiply both sides by.

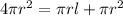
$4\pi r^2=\pi rl+\pi r^2$

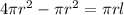
$4\pi r^2-\pi r^2=\pi rl$

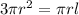
$3\pi r^2=\pi rl$

Cancel out the common factors from both sides.

3r=l

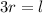
Now, ratio of the radius to the slant height is

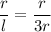
(r)/(l)=(r)/(3r)

(r)/(l)=(1)/(3)

Therefore, the ratio of the radius to the slant height is 1:3.

Please log in or register to add a comment.