Question

A object spins through an angular displacement of 10 radians and has an angular acceleration of 2.3 rad/sec-squared. Assuming it began spinning from rest, over what time interval did the acceleration occur?

Answer 1

The acceleration of the object occurred at 2.95 s

Step-by-step explanation:

Given;

initial angular velocity of the object, ω = 0

angular acceleration, α = 2.3 rad/s²

angular displacement of the object, θ = 10 radians

The time of the motion is given by the following kinematic equation;

θ = ω + ¹/₂αt²

θ = 0 + ¹/₂αt²

θ = ¹/₂αt²

`t^2 = (2 \theta)/(\alpha)\\\\t = \sqrt{(2 \theta)/(\alpha)}\\\\t = \sqrt{(2 *10)/(2.3)}\\\\t = 2.95 \ s`

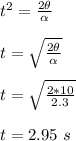
Therefore, the acceleration of the object occurred at 2.95 s