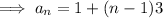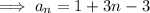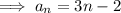Answer:
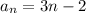
Explanation:
General form of an arithmetic sequence:
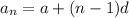
where:
 is the nth term
is the nth term
 is the first term
is the first term
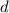 is the common difference between terms
is the common difference between terms
Create expressions for the 4th and 6th terms:
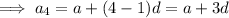
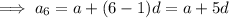
The ratio of the 4th term to the 6th term is 5:8, therefore:
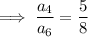



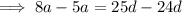
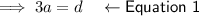
Sum of the first n terms of an arithmetic series:
![S_n=(n)/(2)[2a+(n-1)d]](https://img.qammunity.org/2023/formulas/mathematics/high-school/3xswszu9aa97ib3vxzethlaa34iy1xjgl7.png)
The sum of the first 7 terms of an arithmetic progression is 70:
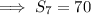
![\implies (7)/(2)[2a+(7-1)d]=70](https://img.qammunity.org/2023/formulas/mathematics/college/ory86pav3jmraggbi4c7krgj1tpfaey1jf.png)
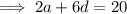
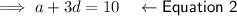
Substitute Equation 1 into Equation 2 and solve for
 :
:
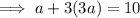
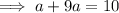

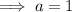
Substitute found value of
 into Equation 1 and solve for
into Equation 1 and solve for
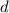 :
:
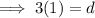
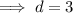
Finally, substitute found values of
 and
and
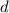 into the general form of the arithmetic sequence:
into the general form of the arithmetic sequence: