Given:
You are given $893 in one, five, and ten dollar bills.
There are 165 bills.
There are twice as many five dollar bills as there are ones and tens combined.
To find:
How many bills of each type are there?
Solution:
Consider the number of bills of one dollars, five dollars and ten dollars are x, y and z respectively.
According to the question,
Number of bills :
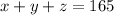 ...(1)
...(1)
Total amount :
 ...(2)
...(2)
Condition :
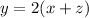 ...(3)
...(3)
Equation (3) can be written as
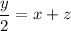 ...(4)
...(4)
Substituting
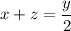 in (1), we get
in (1), we get
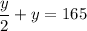
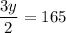
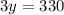
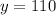
Substituting y=110 in (4), we get
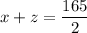
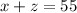
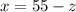 ...(5)
...(5)
Substituting y=110 and x=55-z in (2), we get
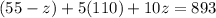
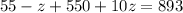

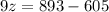

Dividing both sides by 9, we get
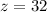
Substituting z=32 in (5), we get
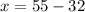
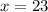
Therefore,
One dollar bills = 23
Five dollars bills= 110
Ten dollars bills = 32