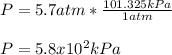Question

What is the pressure in kPa of 2 moles of chlorine gas at a temperature of 5 degrees C

and a volume of 8 dm3?

Answer 1

`P=5.8x10^2kPa`

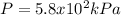
Step-by-step explanation:

Hello.

In this case, since chlorine gas is assumed to behave ideally, we can use the ideal gas equation in order to compute the required pressure:

`PV=nRT`

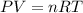
In such a way, since the temperature must be in kelvins and the volume in liters for the universal gas constant:

`T=5+273.15=278.15K\\\\V=8dm^3*(1L)/(1dm^3)=8L`

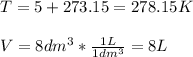
Thus, we first compute the pressure in atm:

`P=(nRT)/(V)= (2mol*0.082(atm*L)/(mol*K)*278.15K)/(8L)\\\\P=5.7atm`

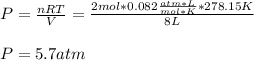
Thus, the pressure in kPa turns out:

`P=5.7atm*(101.325kPa)/(1atm)\\\\P=5.8x10^2kPa`