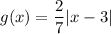Question

NO LINKS!!! Please help me with this graph​

Answer 1

• f(x)=|x|

Find vertex

• f(0)=(0)

So

• (0,0) is the vertex

The graph shifted 3 units right.

So new translation

• g(x)=|x-3|

Find y intercept

• g(0)=|-3|=3

But it's at (0,1) approximately

So compression factor

• 1/3

Now last equation

• g(x)=1/3|x-3|

Accurate one

• Take (-4,2)

Find value

• g(-4)=|-7|=7

So compression factor

• 2/7
• 1/3.5

So accurate equation is

• 1/3.5|x-3|

Answer 2

`g(x)=(2)/(7)|x-3|`

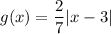
Explanation:

Translations

For
`a > 0`

`f(x-a) \implies f(x) \: \textsf{translated}\:a\:\textsf{units right}`

`y=a\:f(x) \implies f(x) \: \textsf{stretched parallel to the y-axis by a factor of}\:a`

-----------------------------------------------------------------------------------------

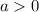
Parent function:
`f(x)=|x|`

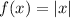
The vertex of the parent function is at (0, 0) as
`f(0)=|0|=0`

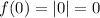
From inspection of the graph, the vertex of the transformed function is at (3, 0). Therefore, there has been a translation of 3 units right:

`\implies g(x)=f(x-3)=|x-3|`

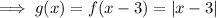
(There has not been any vertical translation since the y-value of the vertex of the parent function and the translated function is the same)

From inspection of the graph, we can see that it has been stretched parallel to the y-axis:

`\implies g(x)=a\:f(x-3)=a|x-3|`

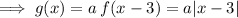
The line goes through points (10, 2) and (-4, 2).

Substituting one of these points to find a:

`\implies a|10-3|=2`

`\implies 7a=2`

`\implies a=(2)/(7)`

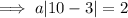
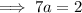
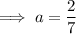
Therefore,

`g(x)=(2)/(7)|x-3|`