Answer:
n = 19
Explanation:
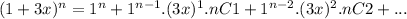
Third term coefficient:
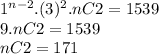
nCr = n!/((n - r)!r!)
nC2 = 171
n!/((n - 2)!2!) = 171
n!/2(n - 2)! = 171
n!/(n - 2)! = 342
n.(n - 1).(n -2).../((n - 2).(n - 3).(n - 4)...) = 342
n(n - 1) = 342
n² - n = 342
(n - ½)² - ¼ = 342
(n - ½)² = 1369/4
(n - ½) = ±37/2
n = 1/2 ± 37/2
n = -18 or n = 19
Since we are told n is a positive integer, it is 19