Answer:
The exact rotation in revolutions per minute is 1.125 revolutions per minute
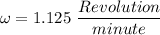
Explanation:
The given angular velocity is expressed as follows;
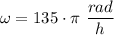
Therefore, we have;
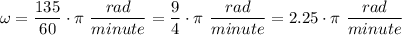
One (1) revolution = 2·π radian
Therefore;
π radian = 1/2 revolution
2.25·π radian = 2.25 × 1/2 revolution = 1.125 revolution
Which gives;
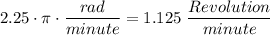
The exact rotations in revolutions per minute is 1.125 revolutions per minute.