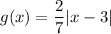Answer:
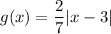
Explanation:
Translations
For
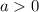


-----------------------------------------------------------------------------------------
Parent function:
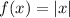
The vertex of the parent function is at (0, 0) as
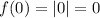
From inspection of the graph, the vertex of the transformed function is at (3, 0). Therefore, there has been a translation of 3 units right:
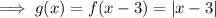
(There has not been any vertical translation since the y-value of the vertex of the parent function and the translated function is the same)
From inspection of the graph, we can see that it has been stretched parallel to the y-axis:

The line goes through points (10, 2) and (-4, 2).
Substituting one of these points to find a:
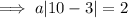
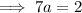

Therefore,