Answer:
Table 3
x | y
50 | 10
60 | 12
70 | 14
80 | 16
Explanation:
x = time in minutes
y = distance travelled
Given that the bike travelled 7 miles after 35 minutes at a constant speed, the rate of change =
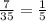 .
.
Thus, the table that represents the relationship between the time in minutes, x, and the distance the bike travles, y would have the same rate of change of ⅕.
Calculate the rate of change of each table using any two given pairs on the table:
Table 1: using (50, 10) and (55, 12)
Rate of change =

Table 2: using (60, 10) and (72, 12)
Rate of change =
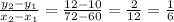
Table 3: using (50, 10) and (60, 12)
Rate of change =
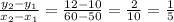
This table has the same rate of change.
Table 4: using (70, 10) and (84, 12)
Rate of change =
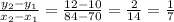
Table 3 represents the relationship between the time in minutes, x, and the distance the bike travles, y.