Answer:
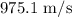 and
and
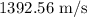
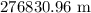
284 seconds
Step-by-step explanation:
(a)
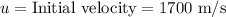
 = Angle of inclination =
= Angle of inclination =
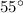
Horizontal velocity is given by
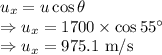
Vertical velocity is given by
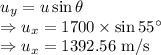
The horizontal and vertical velocities are
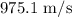 and
and
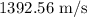 respectively.
respectively.
(b) Range of projectile is given by
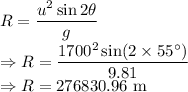
The shell hit the ground
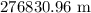 from the launch position.
from the launch position.
(c) Time of flight is given by
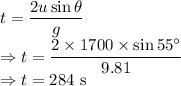
The shell was in the air for 284 seconds.