Answer:
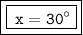
Explanation:
The Given two angles are complementary angles .
The Two angles are 2x° and x°.[Given]
[Two angles are called complementary if their sum is 90°. Each angle is a complement to each other.]
We need to find the value of x.
So,
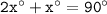
Solve this equation.
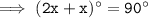
Combine the like terms:
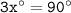
Divide both sides by 3 :

Cancel the LHS and RHS:
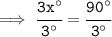

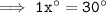
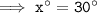
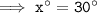
Hence, the value of x° would be 30°.

I hope this helps!