✭ Question -:
A rectangle has a length of (2x+1) units, a width of (x-7) units and an Area of 17 square units. Find the dimensions of the rectangle.
✭ Step-by-step explanation -:
In this question we are provided with the length of a rectangle (2x + 1) units and the width of the rectangle (x - 7). It is also given that the area is 17 units². We are asked to calculate the length and width of the rectangle.
First we will find the value of x
We know,
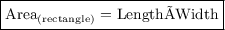
Substituting the values we get
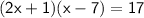
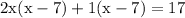
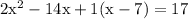
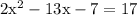
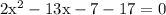
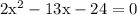
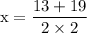
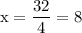
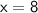
Now we will substitute the value of x
Length = (2x + 1) = 2 × 8 + 1 = 16 + 1 = 17 units
Width = (x - 7) = 8 - 7 = 1 units
- Hence, the length of the rectangle is 17 units and the width is 1 units.