Question

Which phrase describes the geometric interpretation of dividing a complex number z by i?

O Reflect z across the real axis.
O Reflect z across the imaginary axis.
O Rotate z by 90° clockwise about the origin.
O Rotate z by 90° counterclockwise about the origin.

Answer 1

C

Explanation:

rotate Z clockwize

Answer 2

Answer: Rotate z by 90° clockwise about the origin.

Explanation:

Suppose we have the number z = a + b*i, that can be represented with the point (a, b) in a coordinate axis.

If we divide z by i, we have:

`(z)/(i) = (a + b*i)/(i) = (a + b*i)/(i) *(i)/(i) = (a*i - b)/(-1) = b - a*i`

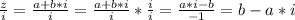
This point will be represented with the point (b, -a)

Then we have the transformation:

(a, b) ----> (b, -a)

This is a rotation of 90° clockwise about the origin.

Then the correct option is:

Rotate z by 90° clockwise about the origin.