Question

A solid metal sphere of radius 9 is melted and transformed into 3 identical spheres. What is the ratio of the surface area of one of these spheres to the surface area of the original sphere?

Answer 1

The ratio is 1 to 2

Explanation:

Volume of the original sphere is ≈ 3,053.63 units³

The surface area of the original sphere is ≈ 1,017.88 units²

Volume of one of the small sphere is ≈ 1,017.88 units³

The radius of one of the small sphere is ≈ 6.24 units

The surface area of one of the small sphere is ≈ 489.3 units²

The ratio of the surface area of one of the small sphere to the surface area of the original sphere is

`(489.3)/(1017.88)` ≈
`(1)/(2)`

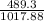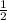
489.3 / 1017.88 ≈ 1 / 2

The ratio is 1 to 2

Answer 2

`243^(2/3):324` or approximately 0.481

Explanation:

Volume of a sphere: 4/3πr³

Surface area of a sphere: 4πr²

The initial sphere of radius 9 has a volume of
`\displaystyle\\9^3\cdot (4)/(3)\cdot \pi=972\pi`

When melted into three identical spheres, each must have a volume of
`\displaystyle (972\pi)/(3)=324\pi`

The radius of the smaller spheres must be:

`(4)/(3)\pi r_s^3=324\pi \implies r_s=\sqrt[3]{243}\approx 6.24`

Surface area of each smaller sphere:

`\displaystyle \\4\pi r^2\vert_(r=6.24)\approx 155.76\pi`

Surface area of initial sphere:

`\displaystyle \\4\pi r^2\vert_(r=9)\approx 324\pi`

The desired ratio is
`155.76/324\approx \boxed{0.481}`

Exact:
`243^(2/3):324`