Answer:
The ratio is 1 to 2
Explanation:
Volume of the original sphere is ≈ 3,053.63 units³
The surface area of the original sphere is ≈ 1,017.88 units²
Volume of one of the small sphere is ≈ 1,017.88 units³
The radius of one of the small sphere is ≈ 6.24 units
The surface area of one of the small sphere is ≈ 489.3 units²
The ratio of the surface area of one of the small sphere to the surface area of the original sphere is
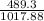 ≈
≈
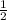
489.3 / 1017.88 ≈ 1 / 2
The ratio is 1 to 2