Hi there!
1)
We can use the following equation to solve for resistivity.
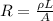
R = Resistance (30 Ω)
ρ = Resistivity (? Ωm)
L = Length (100cm = 1 m)
A = Cross-sectional area of wire (r = 0.15m, A = πr², A = 0.0707 m²)
Rearrange the equation to solve for resistivity.
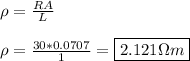
2)
The conductivity of a resistor is equivalent to:
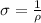
σ = Conductivity (S/m)
ρ = Resistivity (2.121 Ωm)
Solve:
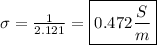
3)
We can use the equation for resistivity to solve. Rearrange the equation for length:
