The
 simplifies to
simplifies to
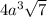 .
.
To simplify
 , you can break down the expression into its prime factorization and then identify the perfect squares.
, you can break down the expression into its prime factorization and then identify the perfect squares.
![\[ √(112a^6) = √(2^4 \cdot 7 \cdot a^6) \]](https://img.qammunity.org/2021/formulas/mathematics/college/74t5mdt5z63sljxi248yyjltiiwcomdvz8.png)
Now, separate the perfect squares and non-perfect squares:
![\[ √(2^4 \cdot 7 \cdot a^6) = √((2^2)^2 \cdot 7 \cdot (a^3)^2) \]](https://img.qammunity.org/2021/formulas/mathematics/college/h460jqz1ofak1twpcgvye6hgfdo75yzbq3.png)
Now, take the square root of the perfect squares:
![\[ 2^2 \cdot a^3 \cdot √(7) \]](https://img.qammunity.org/2021/formulas/mathematics/college/2gponayy40u25fp2d4uu1mnd8tzmd8kzl1.png)
Combine the terms:
![\[ 4a^3 √(7) \]](https://img.qammunity.org/2021/formulas/mathematics/college/wyihlrk56ufuky69plw2bvzzkyzs2xeylg.png)
So,
 simplifies to
simplifies to
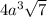 .
.