Question

X+y=1
3y=-3x+3
I don't know how to do this, I have tried everything, please help.

Answer 1

`\begin{cases} x+y=1\\\\ 3y=-3x+3 \end{cases}\hspace{5em}\stackrel{\textit{using the 1st equation}}{x+y=1\implies y=1-x} \\\\\\ \stackrel{\textit{substituting on the 2nd equation}}{3\stackrel{y}{(1-x)}~~ = ~~-3x+3\implies 3-3x=-3x+3}\implies 0~~ = ~~0`

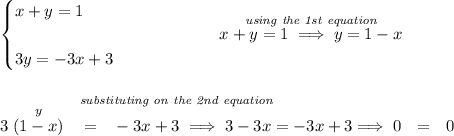
now... the result could have been 3 = 3, or hmmm something like so, which is a bit of a flag hmmm let's take a closer look at the 2nd equation

`\begin{cases} \boxed{x+y=1}\\\\ 3y=-3x+3 \end{cases} \\\\[-0.35em] ~\dotfill\\\\ 3y=-3x+3\implies 3y=3(-x+1)\implies \cfrac{3y}{3}=-x+1 \\\\\\ y=-x+1\implies \boxed{x+y=1}`

let's notice, the 2nd equation is really the 1st one in disguise, so both equations are exactly equal. So what's the solution to that? well, there isn't one solution per se, if we were to graph both lines, it'll be the graph on one line pancaked on top of the other, and where they touch each other is the solution, well, hell they touch each other everywhere, and since both lines go to infinity, then they have infinitely many solutions.