Question

Does anybody know this? I followed the example and did the formula and it told me it was 11.99 but it was wrong. Find the length of the radius if the area of the sector is 361.6 and the central angle is 288 use 3.15 round your answer to the neatest whole number

Answer 1

Hi Student!

The first step that we need to take to solving this problem (and almost any problem), is to concentrate the important information for the problem that is provided. Looking at the problem we can see that we are trying to determine what the length of the radius is. In order to solve this problem we are provided with the area of a sector of 361.6 meters squared and a central angle of 288 degrees.

Now that we have the important information taken care of, we can move onto the part of actually solving the problem. We must first convert our degrees to radians because the equation that we will be using can only use radians for the angle and not degrees. We can simply convert our angle to radians by multiplying it by π/180.

`288\ degrees\ *\ (\pi )/(180\ degrees)`

`288\ degrees\ *\ (3.14)/(180\ degrees)`

`(288\ degrees\ *\ 3.14)/(180\ degrees)`

`5.024\ radians`

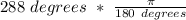
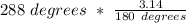
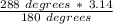
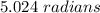
After completing this step, we have converted our degrees to radians and now we can move onto the step where we plug in our information into an equation and solve for our unknown.

`Sector\ Area = radius^2\ *\ (angle)/(2)`

`361.6\ m^2 = radius^2\ *\ (5.024)/(2)`

`361.6\ m^2 = radius^2\ *\ 2.512`

`(361.6\ m^2)/(2.512) = (radius^2\ *\ 2.512)/(2.512)`

`143.949\ m^2 = radius^2`

`√(143.949\ m^2) = √(radius^2)`

`12\ m = radius`

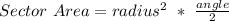
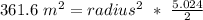
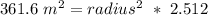
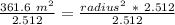
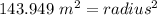
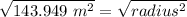
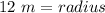
Therefore, after solving our equation for our unknown, we can see that our radius is really close to 12 meters (so we can just round up as the problem stated).