The maximum height of the water balloon : 450 m
Further explanation
Quadratic function is a function that has the term x²
The quadratic function forms a parabolic curve
The general formula is
f (x) = ax² + bx + c
where a, b, and c are real numbers and a ≠ 0.
The parabolic curve can be opened up or down determined from the value of a. If a is positive, the parabolic curve opens up and has a minimum value. If a is negative, the parabolic curve opens down and has a maximum value
So the maximum is if a <0 and the minimum if a> 0.
The formula for finding the coordinates of the maximum and minimum points of the quadratic function is the same.
The maximum / minimum point of the quadratic function is

Where
D = b²-4ac
The function h (t) = -16x²+160x+50
so the value of a <0, then it has a maximum value
Because we are looking for maximum height, then we find the value of the y coordinate, with the formula
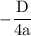
Questions we might add :
What was the maximum height of the water balloon after it was thrown?
We can also use the first derivative of the above function to find the maximum value
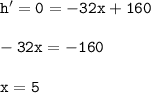
input to function :
