Answer:
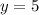 .
.
Or, equivalently:
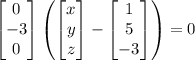 .
.
Explanation:
Every plane in
 could be represented with a vector equation of the form
could be represented with a vector equation of the form
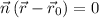 , where:
, where:
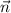 is a vector normal to the plane (a normal vector), and
is a vector normal to the plane (a normal vector), and
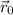 is the position vector of a point in the plane.
is the position vector of a point in the plane.
Notice that in this question, the coordinates (and hence the position vectors) of the points in this plane are already given. For example, the position vector of the point
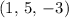 is the vector:
is the vector:
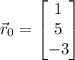 .
.
Specifically in
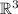 , normal vectors of a plane could be found by:
, normal vectors of a plane could be found by:
- finding two distinct directions parallel to that plane, and
- taking the cross product between the two directions.
Subtracting position vectors of points in this plane from each other would give directions that are parallel to this plane:
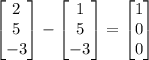 .
.
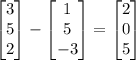 .
.
The cross product between these two vectors in
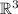 would be:
would be:
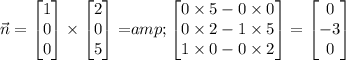 .
.
(Note that the cross product between other directions parallel to the plane might give other normal vectors that are parallel to the one in this example.)
Using the position vector of the point
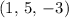 as
as
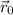 , one possible vector equation for this plane would be:
, one possible vector equation for this plane would be:
 .
.
Expand the dot product and simplify to obtain a scalar equation for this plane:
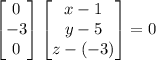 .
.
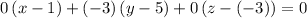 .
.
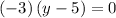 .
.
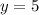 .
.