Question

A 3.3 kg block of copper at a temperature of 74°C is dropped into a bucket containing a mixture of ice and water whose total mass is 1.2 kg. When thermal equilibrium is reached the temperature of the water is 8°C. How much ice was in the bucket before the copper block was placed in it? (Neglect the heat capacity of the bucket.

Answer 1

0.228 kilograms of ice were in the bucket before the copper block was placed in it.

Step-by-step explanation:

In this case, we assume that water inside the bucket was in the form of ice at a temperature of 0 ºC and an atmospheric pressure of 101.325 kilopascals, It is also known that block of copper is cooled down whereas ice is melted and heated up until thermal equilibrium is reached. If ice-block system is an isolated system, then First Law of Thermodynamics depicts the following model:

`-Q_(b) +Q_(l,w)+Q_(s, w) = 0`

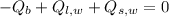
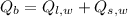`Q_(b) = Q_(l,w)+Q_(s,w)` (Eq. 1)

Where:

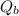`Q_(b)` - Heat released by the block of copper, measured in kilojoules.

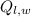`Q_(l,w)` - Latent heat received by water, measured in kilojoules.

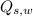`Q_(s,w)` - Sensible heat received by water, measured in kilojoules.

By definitions of sensible and latent heat, we expand the equation as follows:

`m_(b)\cdot c_(b)\cdot (T_(b,o)-T) = m_(w)\cdot [L_(f)+c_(w)\cdot (T-T_(w,o))]` (Eq. 2)

Where:

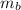`m_(b)` - Mass of the block of copper, measured in kilograms.

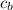`c_(b)` - Specific heat of copper, measured in kilojoules per kilogram-degree Celsius.

`T_(b,o)` - Initial temperature of block of copper, measured in degrees Celsius.

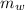`m_(w)` - Mass of water, measured in kilograms.

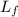`L_(f)` - Latent heat of fusion of water, measured in kilojoules per kilogram.

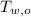`T_(w,o)` - Initial temperature of water, measured in degrees Celsius.

`T` - Final temperature of water-block system, measured in degrees Celsius.

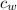`c_(w)` - Specific heat of water, measured in kilojoules per kilogram-degree Celsius

And we clear the mass of water of the system:

`m_(w) = (m_(b)\cdot c_(b)\cdot (T_(b,o)-T))/(L_(f)+c_(w)\cdot (T-T_(w,o)))`

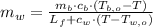
If we know that
`m_(b) = 3.3\,kg`,
`c_(b) = 0.385\,(kJ)/(kg\cdot ^(\circ)C)`,
`T_(b,o) = 74\,^(\circ)C`,
`T = 8\,^(\circ)C`,
`L_(f) = 334\,(kJ)/(kg)`,
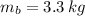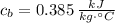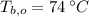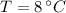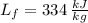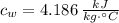`c_(w) = 4.186\,(kJ)/(kg\cdot ^(\circ)C)` and
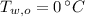`T_(w,o) = 0\,^(\circ)C`, then the mass of the ice inside the bucket is:

`m_(w) = ((3.3\,kg)\cdot \left(0.385\,(kJ)/(kg\cdot ^(\circ)C) \right)\cdot (74\,^(\circ)C-8\,^(\circ)C))/(334\,(kJ)/(kg)+\left(4.186\,(kJ)/(kg\cdot ^(\circ)C) \right)\cdot (8\,^(\circ)C-0\,^(\circ)C) )`

`m_(w) = 0.228\,kg`

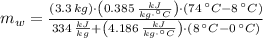
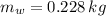
0.228 kilograms of ice were in the bucket before the copper block was placed in it.