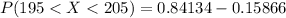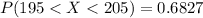Complete Question
A population has a mean of 200 and a standard deviation of 50. Suppose a random sample of 100 people is selected from this population. What is the probability that the sample mean will be within
 of the population mean
of the population mean
Answer:
The value is
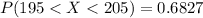
Explanation:
From the question we are told that
The mean is
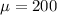
The population standard deviation is
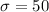
The sample size is
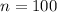
Generally the standard error of sample mean is mathematically represented as

=>
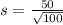
=>
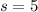
Generally the limits of
 within the population mean is mathematically represented as
within the population mean is mathematically represented as
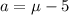
=>
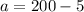
=>
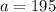
and

=>

=>
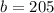
Generally the probability that the sample mean will be within
 of the population mean is mathematically represented as
of the population mean is mathematically represented as
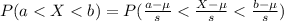
=>
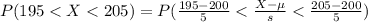
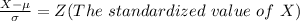
=>
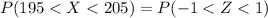
=>
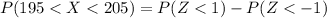
Generally from the z -table the probability of (Z < 1) and (Z<-1 ) is
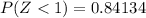
and

So