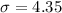Question

A light bulb factory produces 1,409 light bulbs every hour. Approximately 1.36% of the light bulbs are defective, and do not work. Using the binomial distribution, what is the standard deviation of the number of defective bulbs produced in an hour

Answer 1

The value is
`\sigma = 4.35`

Explanation:

From the question we are told that

The number of light bulbs produce every hour is n = 1409

The proportion of light bulbs that are defective is
`p = 0.0136`

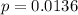
Generally from the question we are told to use binomial distribution hence the standard deviation of the number of defective bulbs produced in an hour is mathematically represented as

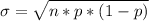
`\sigma = √(n * p * (1- p ))`

=>
`\sigma = √(1409 * 0.0136 * (1 - 0.0136 ))`

=>
`\sigma = 4.35`