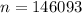Question

A decision maker is interested in estimating the mean of a population based on a random sample. She wants the confidence level to be ​% and the margin of error to be . She does not know what the population standard deviation​ is, so she has selected the pilot sample below. Based on this pilot​ sample, how many more items must be sampled so that the decision maker can make the desired confidence interval​ estimate? The decision maker should sample nothing more items to make the desired confidence interval estimate.

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

The value is
`n = 146093`

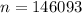
Explanation:

From the question we are told that

The margin of error is
`E = 0.04`

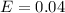
The data is

8.70 4.79 10.95 15.19 14.06

16.99 1.22 9.02 14.39 5.73

7.28 3.22 2.66 6.13 6.93

Generally the sample mean is mathematically represented as

`\= x = (\sum x_i)/(n)`

=>
`\= x = ( 8.70 + 4.79 +\cdots + 6.93)/(15)`

=>
`\= x = 8.48`

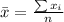
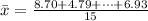
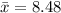
Generally the standard deviation is mathematically represented as

`\sigma = \sqrt{ ( \sum (x_i - \= x))/(n) }`

=>
`\sigma = \sqrt{ ( (8.70 - 8.48 )^2 + ( 8.70 - 8.48)^2 + \cdots + (6.93 - 8.48)^2 )/(15) }`

=>
`\sigma = 5.14`

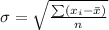
From the question we are told the confidence level is 98% , hence the level of significance is

`\alpha = (100 - 98 ) \%`

=>
`\alpha = 0.02`

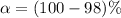
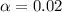
Generally the degree of freedom is mathematically represented as

`df = n -1`

=>
`df = 15 -1`

=>
`df = 14`

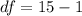
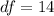
Generally from the t distribution table the critical value of at a degree of freedom of is

`t_{(\alpha )/(2) ,  14 } = 2.9768`

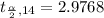
Generally the sample size is mathematically represented as

`n =[ \frac{t_{(\alpha )/(2) , 14 } * \sigma }{E} ]^2`

=>
`n =[ ( 2.9768 * 5.136 )/(0.04) ]^2`

=>
`n = 146093`