Question

A decision maker is interested in estimating a population proportion. A sample of size n150 yields 115 successes. Based on these sample​ data, construct a​ 90% confidence interval estimate for the true population proportion. A. ​(0.714, 0.826) B. ​(0.717, 0.823) C. ​(0.750, 0.790) D. ​(0.737, 0.803)

Answer 1

A. ​(0.714, 0.826)

Explanation:

Given that:

The sample size n = 150

The number of success(sample proportion) x = 115

The population proportion
`\hat p` =
`(x)/(n)`

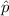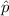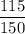
The population proportion
`\hat p` =
`(115)/(150)`

The population proportion
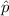`\hat p` = 0.767

At 90% confidence interval level;

`Z_(\alpha /2) = Z_(0.05) = 1.645`

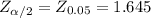
Thus, the confidence interval estimate for the true population proportion can be computed by using the formula:

`=\hat p \ \pm \ z_(\alpha /2) \sqrt{(\hat p(1- \hat p))/(n) }`

`= 0.767 \ \pm 1.645 * \sqrt{(0.767(1- 0.767))/(150) }`

`= 0.767 \ \pm 1.645 * \sqrt{(0.767(0.233))/(150) }`

`= 0.767 \ \pm 1.645 * \sqrt{(0.178711)/(150) }`

`= 0.767 \ \pm 1.645 * √(.0011914)`

`= 0.767 \ \pm 1.645 * 0.03452`

`= 0.767 \ \pm 0.0568`

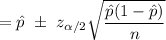
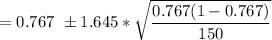
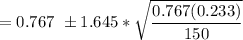
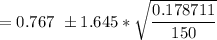
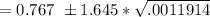
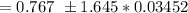
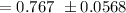
= (0.767 - 0.0568, 0.767 + 0.0568)

= (0.7102 , 0.8238 )

Due to approximation; the confidence interval estimate for the true population proportion is
`\simeq` ​(0.714, 0.826)