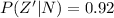Question

A company has 2 machines that produce widgets. An older machine produces 23% defective widgets, while the new machine produces only 8% defective widgets. Besides, the new machine produces 3 times as many widgets as the older machine does. Given that a randomly chosen widget was tested and was found to be defective, what is the probability that it was produced by the new machine

Answer 1

The value is
`P(Z' | N )= 0.92`

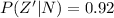
Explanation:

From the question we are told that

The proportion of defective widgets produced by older widget is
`p = 23\% = 0.23`

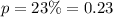
The proportion of defective widgets produced by new widget is

`q = 0.08`

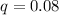
Generally since we are considering the new machine in this question it then mean that the probability that widget was defective given that it was produce by the new machine is

`P(Z | N ) = 0.08`

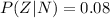
Here Z is the event that the widget was defective

N is the even that the widget was produced by the new machine

Also the probability that the widget was defective given that it was not produced by the new machine is

`P(Z | N') = 0.23`

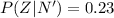
Generally from the question the probability that the widget was produced by the new machine is mathematically represented as

`P( N) = (3)/(4)`

=>
`P( N) = 0.75`

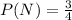
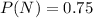
Generally the probability that the widget is defective and that it was produced by the new is mathematically represented as

`P( Z\ n \ N) = P(Z | N ) * P(N)`

=>
`P( Z\ n \ N) = 0.08 * 0.75`

=>
`P( Z\ n \ N) = 0.06`

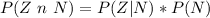
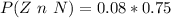
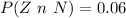
Generally the probability that the widget is defective and that it was not produced by the new machine is

`P(Z\ n \ N') = P( Z | N' ) * [1 -P(N)]`

=>
`P(Z\ n \ N') = 0.23 * [1 -0.75]`

=>
`P(Z\ n \ N') =0.0575`

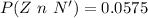
Generally the probability that the widget is defective is

`P(Z) = P(Z \ n \ N) + P(Z \ n \ N')`

=>
`P(Z) = 0.06 + 0.0575`

=>
`P(Z) = 0.1175`

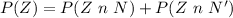
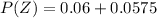
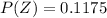
Generally the probability that the widget is not defective and it produced by the new machine is mathematically represented as

`P(Z' \ n \ N ) = P(N ) - P(Z \ n \ N)`

=>
`P(Z' \ n \ N ) =0.75 - 0.06`

=>
`P(Z' \ n \ N ) =0.69`

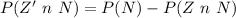
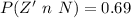
Generally the probability that the widget was produced by the new machine,given that a randomly chosen widget was tested and was found to be defective is mathematically represented as

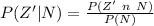
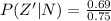
`P(Z' | N ) =(P(Z' \ n \ N))/(P(N))`

=>
`P(Z' | N )= (0.69)/(0.75)`

=>
`P(Z' | N )= 0.92`