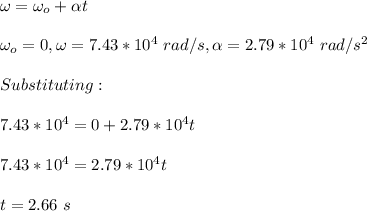Answer:
2.66 s
Step-by-step explanation:
Given The initial angular speed (
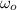 ) = 1.34 x 10⁴ rad/s, the final angular speed (ω) = 4.37 x 10⁴ rad/s, the angular acceleration (α), distance (θ) = 3.10 x 10⁴ rad.
) = 1.34 x 10⁴ rad/s, the final angular speed (ω) = 4.37 x 10⁴ rad/s, the angular acceleration (α), distance (θ) = 3.10 x 10⁴ rad.
Using the formula:
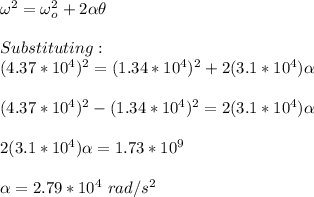
The constant acceleration = 2.79 * 10⁴ rad/s.
Since there is constant acceleration, to reach a final speed of 7.43 x 10⁴ rad/s, we use the formula: