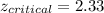Question

A random sample of 114 observations produced a sample mean of 30. Find the critical and observed values of z for the following test of hypothesis using The population standard deviation is known to be 5 and the population distribution is normal.

Answer 1

Complete Question

A random sample of 114 observations produced a sample mean of 30. Find the critical and observed values of z for the following test of hypothesis using α=0.01. The population standard deviation is known to be 5 and the population distribution is normal.

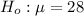`H_o: \mu =28` versus H1: μ>28.

Round your answers to two decimal places.

`z_(critical) =`

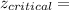
Answer:

`z_(critical) = 2.33`

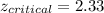
The observed value is
`z = 4.27`

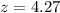
Explanation:

From the question we are told that

The sample size is n = 114

The sample mean is
`\= x   =  30`

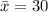
The significance level is
`\alpha = 0.01`

The population standard deviation is
`\sigma = 5`

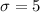
The null hypothesis is
`H_o: \mu =28`

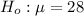
The alternative hypothesis is H1: μ>28.

Generally the test statistics (observed value ) is mathematically represented as

`z = ( \= x - \mu )/( (\sigma )/(√(n) ) )`

=>
`z = ( 30- 28 )/( (5)/(√(114) ) )`

=>
`z = 4.27`

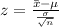
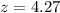
From the normal distribution table the critical value of
`\alpha = 0.01` is

`z_(critical) = 2.33`