Question

Given the following probability distributions:

Distribution C X P{X = Xi)
0 1 2 3 4
0 0.20 0.20 0.20 0.20
Distribution D X P{X = Xi)
0 1 2 3 4
0 0.10 0.40 0.20 0.10
A. Compute the expected value for each distribution.
B. Compute the standard deviation for each distribution.
C. Compare the results of distributions C and D.

Answer 1

Explanation:

The expected value of this distribution will be the Mean

upon calculation

For the distribution of C

1) P(x=xi) 0 1 2 3 4

0 0.20 0.20 0.20 0.20

`Mean = Pi*xi`

= 0*0+1*0.2+2*0.2+3*0.2+4*0.2

Mean = 2

2) Standard deviation of C

`√((xi-mean)^2 *P(xi))`

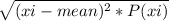
= 1.09

For the distribution of D

1) P(x=xi) 0 1 2 3 4

0 0.1 0.4 0.2 0.1

`Mean = Pi*xi`

= 1.9

2) Standard deviation

= 0.984

Upon comparing the result we observe that

C has greater expected value than D

C has greater standard deviation than D which means it is more spreading of the given data than D.