Answer: 0.8185
Explanation:
Let X represents the tree diameters that are distributed normally.
Given: Mean
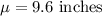 , Standard deviation
, Standard deviation
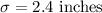
The probability that its diameter will fall between 7.2 inches and 14.4 inches will be:
![P(7.2<X<14.4)=P((7.2-9.6)/(2.4)<(X-\mu)/(\sigma)<(14.4-9.6)/(2.4))\\\=P(-1<Z<2)\ \ \ \ [Z=(X-\mu)/(\sigma)]\\\\=P(Z<2)-P(Z<-1)\\\\=P(Z<2)-(1-P(Z<1))\\\\=0.9772-(1-0.8413)=0.8185\ [\text{By p-value table}]](https://img.qammunity.org/2021/formulas/mathematics/college/dim4cdtdi5nrsmldmexx048bih4zuohn5l.png)
Hence, required probability = 0.8185